Minio基础 - Minio纠删码
Minio基础 - Minio纠删码
Minio使用纠删码
erasure code和校验和checksum来保护数据免受硬件故障和无声数据损坏。 即便您丢失一半数量(N/2)的硬盘,您仍然可以恢复数据。
1. 什么是纠删码erasure code?
纠删码是一种恢复丢失和损坏数据的数学算法, Minio采用Reed-Solomon code将对象拆分成N/2数据和N/2 奇偶校验块。 这就意味着如果是12块盘,一个对象会被分成6个数据块、6个奇偶校验块,你可以丢失任意6块盘(不管其是存放的数据块还是奇偶校验块),你仍可以从剩下的盘中的数据进行恢复
2. 为什么纠删码有用?
纠删码的工作原理和RAID或者复制不同,像RAID6可以在损失两块盘的情况下不丢数据
而Minio纠删码可以在丢失一半的盘的情况下,仍可以保证数据安全。
而且Minio纠删码是作用在对象级别,可以一次恢复一个对象,而RAID是作用在卷级别,数据恢复时间很长。
Minio对每个对象单独编码,存储服务一经部署,通常情况下是不需要更换硬盘或者修复。Minio纠删码的设计目标是为了性能和尽可能的使用硬件加速。
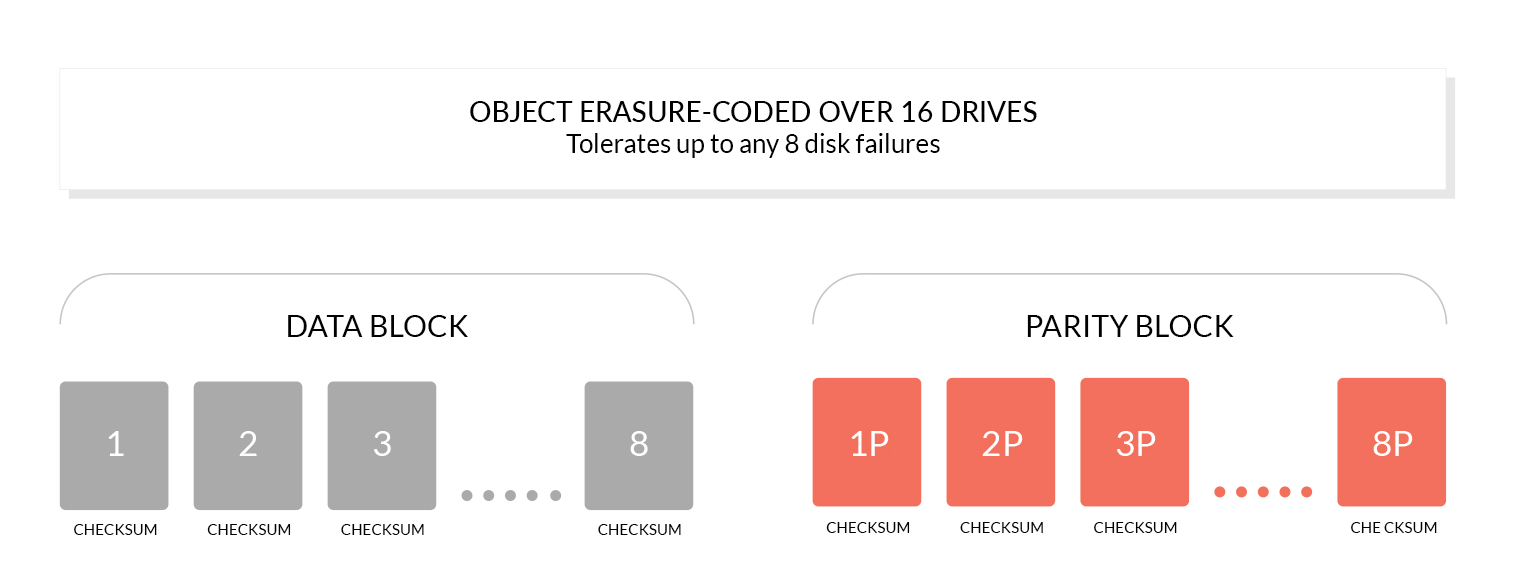
3. 什么是位衰减bit rot保护?
位衰减又被称为数据腐化Data Rot、无声数据损坏Silent Data Corruption,是目前硬盘数据的一种严重数据丢失问题。硬盘上的数据可能会神不知鬼不觉就损坏了,也没有什么错误日志。正所谓明枪易躲,暗箭难防,这种背地里犯的错比硬盘直接咔咔宕了还危险。 不过不用怕,Minio纠删码采用了高速 HighwayHash 基于哈希的校验和来防范位衰减。
4. 更深入的理解
4.1 数据冗余技术
副本策略和纠删码是存储领域常见的两种数据冗余技术。相比于副本策略,纠删码具有更高的磁盘利用率。 Reed-Solomon码是一种常见的纠删码。
4.1.1 纠删码 Erasure Code
Erasure Code是一种编码技术,它可以将n份原始数据,增加m份数据,并能通过n+m份中的任意n份数据,还原为原始数据。即如果有任意小于等于m份的数据失效,仍然能通过剩下的数据还原出来。
纠删码技术在分布式存储 系统中的应用主要有三类,
- 阵列纠删码(Array Code: RAID5、RAID6等)
- RS(Reed-Solomon)里德-所罗门类纠删码
- LDPC(LowDensity Parity Check Code)低密度奇偶校验纠删码。 LDPC码目前主要用于通信、视频和音频编码等领域。
纠删码技术主要是通过纠删码算法将原始的数据进行编码得到冗余,并将数据和冗余一并存储起来,以达到容错的目的。其基本思想是将n块原始的数据元素通过一定的计算,得到m块冗余元素(校验块)。对于这n+m块的元素,当其中任意的m块元素出错(包括原始数据和冗余数据)时,均可以通过对应的重构算法恢复出原来的n块数据。
- 生成校验的过程被成为编码(encoding)
- 恢复丢失数据块的过程被称为解码(decoding)。磁盘利用率为n/(n+m)。
基于纠删码的方法与多副本方法相比具有冗余度低、磁盘利用率高等优点。
4.1.2 多副本策略
多副本策略即将数据存储多个副本(一般是三副本,比如HDFS),当某个副本丢失时,可以通过其他副本复制回来。三副本的磁盘利用率为1/3。
4.1.3 两种冗余技术对比
| 两种技术 | 磁盘利用率 | 计算开销 | 网络消耗 | 恢复效率 |
|---|---|---|---|---|
| 多副本(3副本) | 1/3 | 几乎没有 | 较低 | 较高 |
| 纠删码(n+m) | n/(n+m) | 高 | 较高 | 较低 |
工程实践中,一般对于热数据还是会使用多副本策略来冗余,冷数据使用纠删码。
4.2 Reed-Solomon(RS)码
Reed-Solomon(RS)码是存储系统较为常用的一种纠删码,它有两个参数n和m,记为RS(n,m)。n代表原始数据块个数。m代表校验块个数。接下来介绍RS码的原理。
4.2.1 RS码原理
以n=5,m=3为例。即5个原始数据块,乘上一个(n+m)*n的矩阵,然后得出一个(n+m)*1的矩阵。根据矩阵特点可以得知结果矩阵中前面5个值与原来的5个数据块的值相等,而最后3个则是计算出来的校验块。
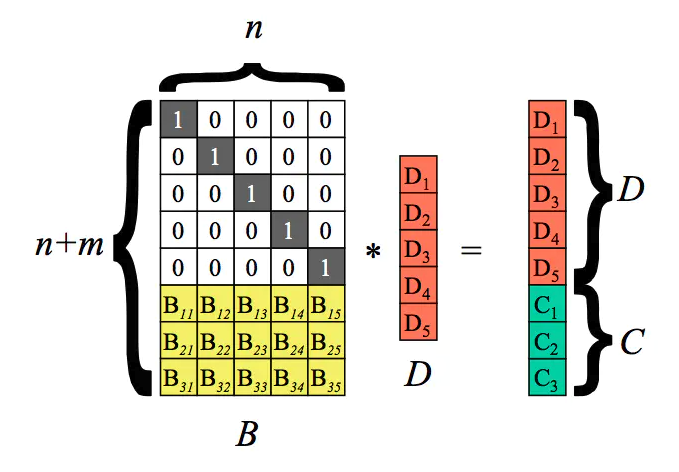
以上过程为编码过程。D是原始数据块,得到的C为校验块。
4.2.2 丢失了m块数据
假设丢失了m块数据。如下:
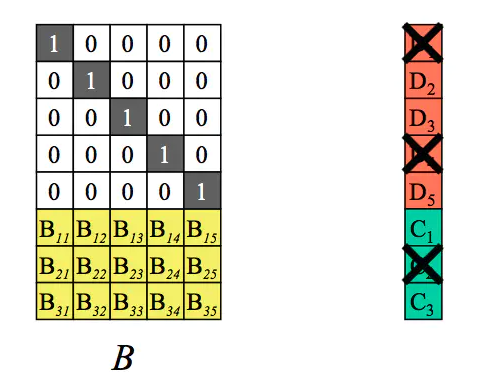
那我们如何从剩余的n个数据块(注意,这里剩余的n块可能包含几个原始数据块+几个校验块)恢复出来原始的n个数据块呢,就需要通过下面的decoding(解码)过程来实现。
4.2.2.1 第一步:删除丢失的行
第一步:从编码矩阵中删去丢失数据块和丢失编码块对应行。 将删掉m个块的(n+m)1个矩阵变形为n1矩阵,同时B矩阵也需要删掉对应的m个行得出一个B'的变形矩阵,这个B'就是n*n矩阵。如下:假设D1、D4、C2丢失,我们得到如下B’矩阵及等式。
4.2.2.2 第二步:求出B’的逆矩阵。
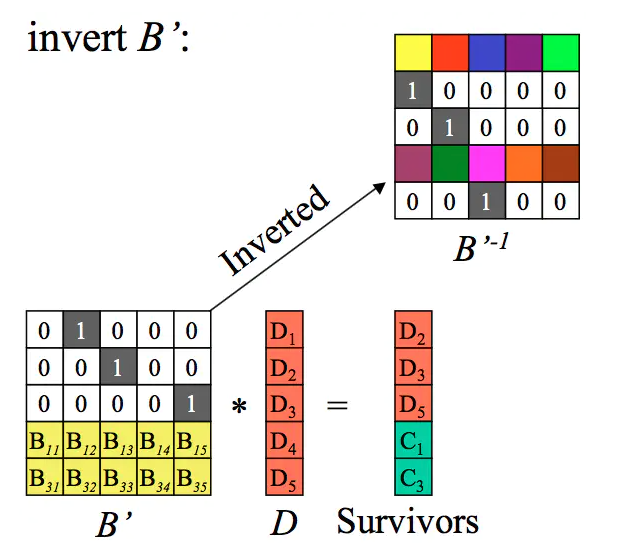
4.2.2.3 第三步:等式两边分别乘上B’的逆矩阵。
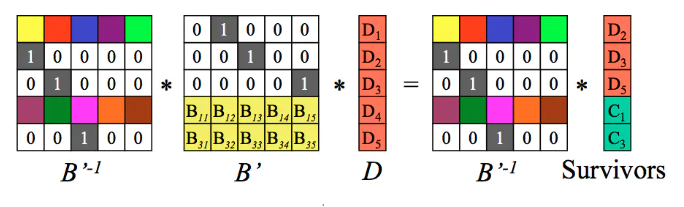
B’和它的逆矩阵相乘得到单位矩阵I,如下:
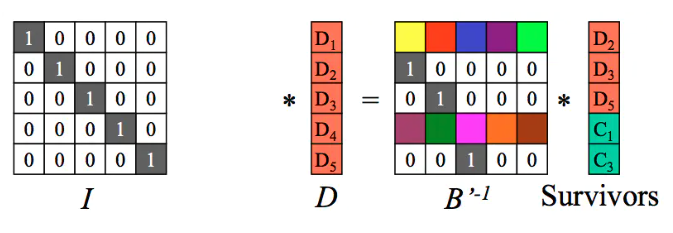
左边只剩下原始数据矩阵D:
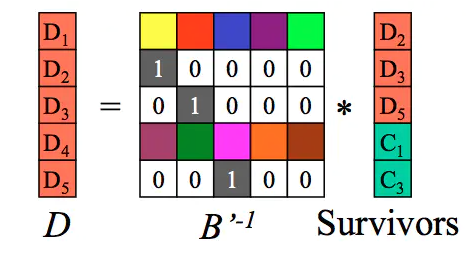
至此完成解码过程。
注:图中黄色部分为范德蒙矩阵。至于如何生成B矩阵,以及如何求B’的逆矩阵,请查看其他相关文献,这里不再赘述。
4.2.3 RS的特点
- 低冗余度,高磁盘利用率。
- 数据恢复代价高。 丢失数据块或者编码块时, RS需要读取n个数据块和校验块才能恢复数据, 数据恢复效率也在一定程度上制约了RS的可靠性。
- 数据更新代价高。 数据更新相当于重新编码, 代价很高, 因此常常针对只读数据,或者冷数据。
4.3 纠删码优/劣势
4.3.1 优势
纠删码技术作为一门数据保护技术,自然有许多的优势,首先可以解决的就是目前分布式系统,云计算中采用副本来防止数据的丢失。副本机制确实可以解决数据丢失的问题,但是翻倍的数据存储空间也必然要被消耗,这一点却是非常致命的。EC技术的运用就可以直接解决这个问题。
4.3.2 劣势
EC技术的优势确实明显,但是他的使用也是需要一些代价的,一旦数据需要恢复,他会造成2大资源的消耗:
- 网络带宽的消耗,因为数据恢复需要去读其他的数据块和校验块
- 进行编码,解码计算需要消耗CPU资源
就是既耗网络又耗CPU
4.3.3 总结
最好的选择是用于冷数据集群,有下面2点原因可以支持这种选择
- 冷数据集群往往有大量的长期没有被访问的数据,体量确实很大,采用EC技术,可以大大减少副本数
- 冷数据集群基本稳定,耗资源量少,所以一旦进行数据恢复,将不会对集群造成大的影响